베르누이방정식(Bernoulli's equation)
1 베르누이방정식
1) 정의
- 정상유동에서 유선을 따라 이동하는 유체를 오일러방정식을 이용하여 유체거동을 단순화한 식.
- 에너지보존법칙을 응용한 변형식이며 뉴턴의 제2법칙의 변형식으로 볼 수 있다.
* 베르누이방정식을 일반화 한것이 나비에 스톡스 방정식이다.(Navier-Stokes equations)
2) 전제조건
- 유선을 따라서 유동
* 유선(streamline)이 경계층을 통과해서는 안 된다. 단, 비회전성 유동일 경우에는 상관없다.
- 유체는 비점성(마찰이 없음)
- 정상유동
* 시간에 대한 변화가 없어야 함. 정상 상태(steady state).
- 비압축성 유체 → 오일러방정식에서 추가된 조건
* 유체는 비압축성이어야 한다. 압력이 변해도 밀도가 변하지 않아야 한다.
2 베르누이방정식의 유도
- 오일러 유체운동방정식
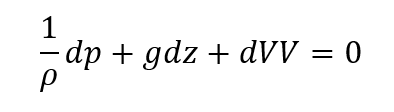
- 오일러 방정식의 적분

- 전제조건 : 비압축성 유체
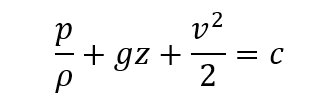
* ρ = c
- 베르누이방정식
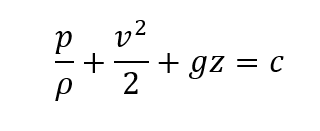

* v : 유선 내 특정지점 유동 속도
* g : 중력 가속도
* h : 높이
* p : 유선 내 특정지점 압력
* ρ : 유체의 밀도
- 위치조건(수두)로 변환
3 베르누이방정식의 활용
1) 유체 속도 계산
- 오리피스/사이펀/피토관의 계산
2) 물리적현상 설명
- 매그누스 현상
- 사이펀현상
3) 활용의 한계
- 베르누이의 정리는 점성이 없는 유체에서만 성립하는데 점성이 없는 유체는 없고 오직 이상기체에서만 성립한다.
- 비압축성의 전제는 오직 액상의 물체에서만 성립되어 기체상의 유체에서는 상당한 오차가 발생한다.