1 단면계수(Z ; section modulus)
1) 단면모멘트와 단면계수
- 단면계수는 단면의 형태에 영향을 받으며 재료는 영향을 미치지 않는다.
- 도형 내 미소면적과 중립축의 거리를 곱한값의 합을 단면 1차모멘트라한다.
- 도형 내 미소면적과 중립축의 거리의 제곱을 곱한값의 합을 단면 2차모멘트라한다.
- 단면계수는 단면 2차 모멘트를 통해서 구한다.
- 도심축에 대한 단면이차모멘트를 단면의 가장 끝단에서 도심까지의 거리로 나눈값이다.


2) 단면계수의 특징
- 보의 굽힘강도를 측정하는데 사용된다.
- 단면의 형태에 의해 결정된다.
- 보의 변형력은 인장과 압축에 영향을 받지 않는 중립축에서의 거리에 비례하며 중립축에서 가장 먼 부분이 최대값을 가진다. 이때의 최대값을 단면계수로 본다.
3) 단면계수의 활용
- 단면계수가 클수록 굽힘강도가 커져서 안정적인 단면이라할 수 있다.
* 최외각거리가 짧을수록, 관성모멘트가 클수록 굽힘에 안정적인 단면이다.
* 최외곽거리는 도심축으로부터 가장 외각의 거리를 뜻함.
2 극단면계수(Zp ; polar modulus of section) 와 극단면2차모멘트(Ip)
참고) 접두어 '극' - 접두로 극이 붙는 개념은 휨이 아닌 비틀림을 계산할때 사용하는 것으로 가로 세로 방향과 무관한 상태를 만들기 위함이다.
1) 극단면계수의 정의
- 비틀림의 저항에 대한 수치적 정도.
- 단면계수의 x, y축 방향의 값을 합한 것으로 비틀림을 계산하기 위해 계산한다.
* 비틀림은 전단응력의 일종으로 Zp가 클수록 물체의 전단응력이 커진다.

2) 극단면 2차모멘트(극관성모멘트 Ip)
- 물체의 회전강성(비틀림에 대한 저항)을 구하기 위해 사용된다.
- 극관성모멘트 값이 클수록 비틀림에 대한 저항이 커져서 구조적으로 안전하다고 볼 수 있다.
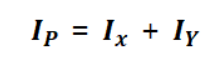
3) 극단면계수와 극단면2차모멘트의 관계
- 극단면2차모멘트는 극단면계수를 구하기 위한 중간 단계이다.
- 극단면계수를 통해 비틀림힘(토오크)와 전단력의 상관관계를 표현한다.
'기계공학 > 기계역학' 카테고리의 다른 글
| 냉동사이클 (0) | 2024.07.18 |
|---|---|
| 유체유동(유체경계층 / 속도경계층) (0) | 2024.07.18 |
| 내부에너지와 엔탈피 (0) | 2024.07.11 |
| 영율(young's modulus) (0) | 2024.07.08 |
| 실속(stall) (0) | 2024.07.03 |