1 편미분
1) 정의
- 다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 간주하여 미분하는 것이다.
- 변수가 여러개인 다변함수를 하나의 변수에 대해 미분하는것.
2) 의미
- 대상이되는 변수 외의 변수를 상수로 갖ㄴ주한뒤 미분해 얻은 도함수를 편도함수라한다.
* 편미분을 진행한 함수를 편도함수라한다.
- 특정한 파라미터의 작은 변화가 전체적인 결과에 어떠한 영향을 미치는지 예측할때 사용됨
3) 관련공식
- x, y 2개의 변수로 이후어진 변수에 대해 아래처럼 나타낼 수 있다.
- y를 고정하였을대 x에 대한 f(x,y)의 변화비율
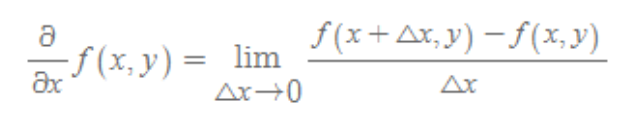
2 전미분
1) 정의
- 다변수 함수의 모든 변수의 변화에 따라 변화하는 행태를 근사하는 양이다.
* 전미분은 다변수 함수의 증분의 주요 선형 부분이다.
* 변수 하나의 변화만을 생각하는 편미분과 달리, 모든 변수의 변화를 더불어 생각한다.
- x에 의한 편미분에 x의 미소한 변화량을 곱한것과, y에 의한 편미분에 y의 미소변화량을 곱한것을 더한것.
2) 의미
- 모든 파라미터가 변할때 전체적인 결과에 어떤 영향을 미치는지 알 수 있음.
3) 특징
- 모든 변수에 대해 편미분 가능하고, 모든 편미분 연속 함수라면, 전미분 가능 함수이다. 이 경우 함수가 연속 미분 가능하다고 한다.
- 전미분 가능 함수는 항상 연속 함수이다.
- 전미분 가능 함수는 항상 모든 변수에 대해 편미분 가능하다.
- 전미분 가능 함수는 항상 모든 방향에 대해 방향 미분 가능하다.
4) 관련식
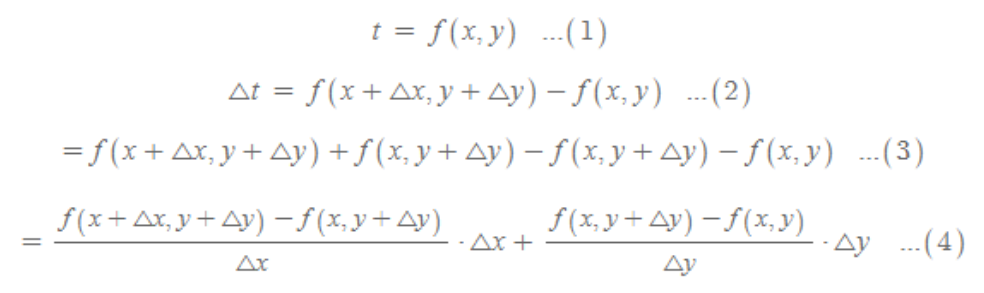
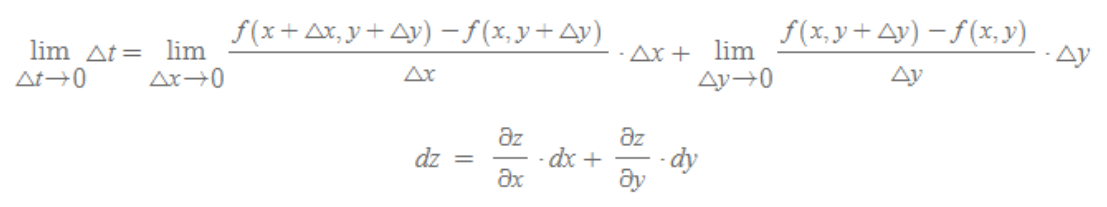
'트랜드 > 일반과학' 카테고리의 다른 글
| 벡터의 연산 (0) | 2025.04.22 |
|---|---|
| 핵폐기물 (1) | 2024.12.05 |
| 4대 기본 힘(강력/약력/전자기력/중력) (0) | 2024.07.26 |
| 금속 원자 결합의 종류 (0) | 2024.07.06 |
| 자성체의 종류와 특징 (0) | 2024.06.27 |