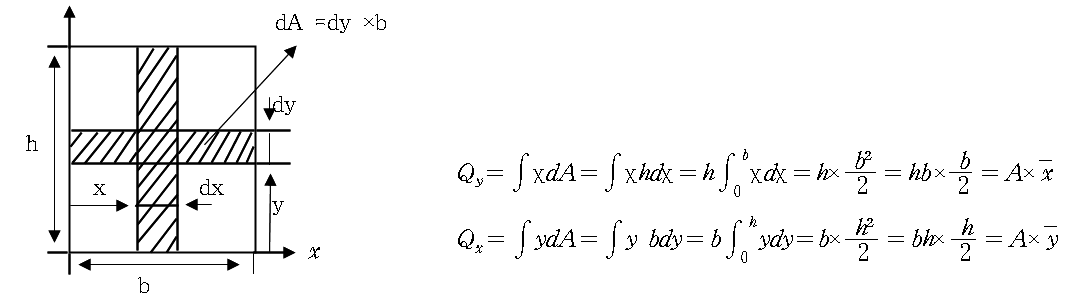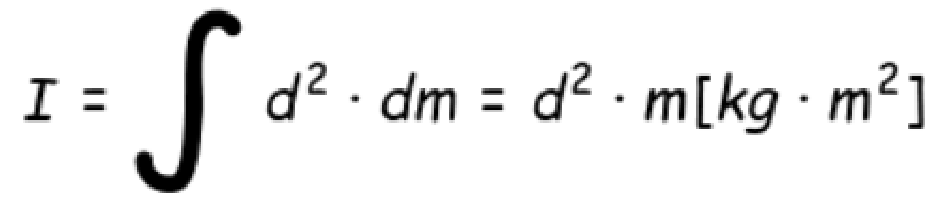1 단면1차모멘트(G ; statical moment of area)
1) 단면1차모멘트의 정의
- 축으로부터 도심까지의 거리에 면적을 곱한것으로 단위는 길이의 세제곱이다.
- 도심은 모멘트가 0인 물체의 중심
* 물체를 회전하기 위해 필요한 힘이 최소인 곳
* 단면 1차모멘트가 0이되는 지점.
* 직교 좌표축에서 도심까지의 거리는 단면1차모멘트에 도형의 면적으로 나누면 구할 수 있다.
- 단면1차모멘트는 평면도형의 도심을 구하기 위해 사용된다.
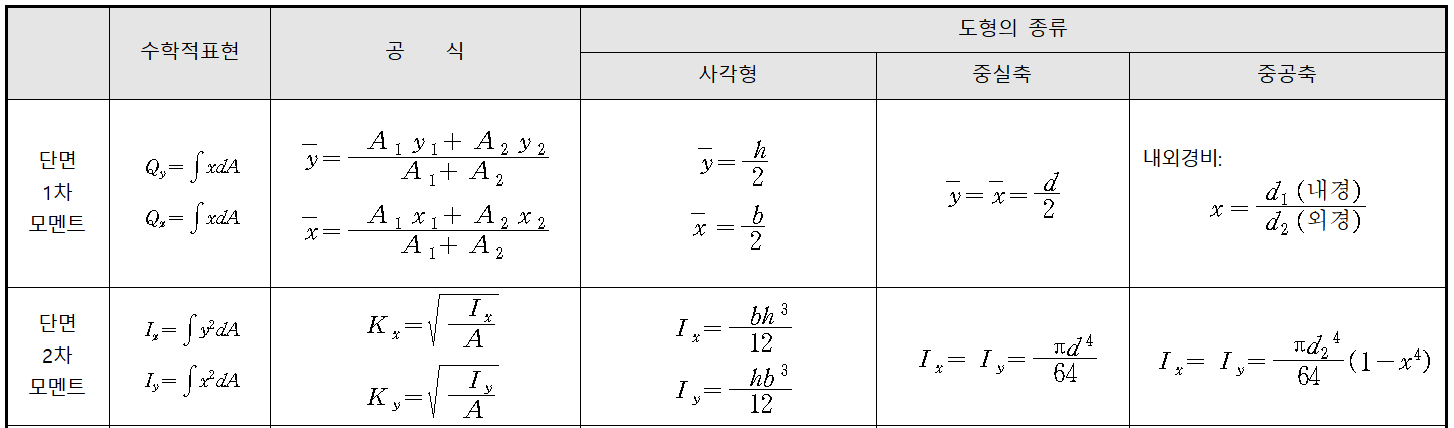
2) 단면1차모멘트의 계산
2 단면2차모멘트(I ; area moment of inertia)
1) 강체운동
- 강체의 운동은 병진운동과 회전운동으로 구분된다.
* 병진운동에 대한 관성을 표시하는 양은 질량
* 회전운동에 대한 관성을 나타내는 양을 관성모멘트
2) 단면2차모멘트(단면관성모멘트)의 정의
- 단면2차 모멘트, 단면 관성 모멘트 : 휘어짐에 저항하는 개념을 수치화한 것.
- 단면2차 모멘트를 구하는 목적은 휨을 받는 축이나 구조물의 휨에대한 강성을 알기 위해서이다.
* 단면2차 모멘트는 단면이 벤딩축으로 상대적으로 얼마나 잘 퍼져있느냐에 비례
- 재료에 외력이 가해져 굽힘등의 변형이 발생할때 재료의 단면적이 일정한 경우 발생하는 응력은 동일하나, 재료 단면의 형상에 따라 굽힘의변형정도가 달라지므로 단면2차모멘트가 클수록 굽힘에 강한재료라 할 수 있다.
참고) 질량관성모멘트와 단면관성모멘트는 다른 개념이다. 수식은 유사하나 단위와 사용이 다르다.
* 질량관성모멘트(mass moment of ineria)는 회전운동 상태를 유지하려는 저항을 의미한다.
일반적으로 관성모멘트라고 표현한다. 단위 kg㎡
* 단면관성모멘트는(area moment of inertia)는 휘어짐에 대한 저항을 의미한다.
단면2차모멘트라고 표현한다.
3) 단면2차모멘트의 계산
3 관성모멘트(mass moment of ineria)
1) 관성모멘트의 정의
- 한 물체에 대해 회전하는 정도를 변화시키는 돌림힘의 양.
- 질량 및 회전축에 대한 물체의 질량 분포에 의해 결정된다.
- 돌림힘에 대해 각속도 변화를 일으키기 어려운 정도가 관성모멘트이다.
- 단위는 kg㎡ 로 표시된다.
- 밀도가 일정하고 모양이 같은 두 물체에 대해서는 질량이 더 큰 쪽이 질량이 같다면 회전축에 더 멀리 분포된 부분이 많은 쪽이 관성모멘트가 더 크다.
- 같은 물체라도 회전축에 따라 값이 달라진다.
2) 관성모멘트의 계산
'기계공학 > 기계역학' 카테고리의 다른 글
| 마찰(friction) (0) | 2025.01.14 |
|---|---|
| 크리프(재료역학측면) (0) | 2025.01.13 |
| 재료의 파손 학설 (0) | 2025.01.09 |
| 충격하중과 정하중의 관계(증명) (0) | 2025.01.08 |
| 열역학적 함수(과정) (0) | 2025.01.07 |